Visualizing Kant's Architectonic Tables

This page features visualizations of the relations between individual elements within Kant's architectonic tables. Alongside these visualizations, I include annotated versions of these tables to help explain the items in the nodes of the visualizing diagrams. Some of these diagrams can get especially large, so for ease of visualization and readability, you can find them in .pdf form here.

This first diagram shows connections between individual concepts of reflection, logical functions of the understanding, and logical forms of judgment. Each first and second function treats representations according to the first and second corresponding concepts of reflection, while the third function treats representations according to both concepts of reflection.

Each logical form is generated by applying the corresponding function to order conceptual representations (concepts and judgments).

Note that the first element in each table (be it a concept of reflection, a logical function, or logical form) conditions the ones that follow (as indicated by dotted arrows). The second element opposes the first one (as indicated by the red dotted arrow), and the third element (when available) combines aspects of the first and second elements (as indicated by the two dotted arrows going to it from the first two elements).

The diagram below adds connections depicting the progression from headings of Quantity to Quality to Relation to Modality (in the form of thin reverse dotted arrows) across functions, forms, and categories. The basic idea is roughly that:

Quantity: determines a domain of representations for the activities of our spontaneous cognition (i.e., the quantity of representations to then give a quality, and then relate to each other and to our spontaneous capacity for cognition)

Quality: determines qualities of quantitatively determined representations

Relation: determines relations between quantitatively and qualitatively determined representations

Modality: determines relations between our spontaneous capacity for cognition in general and quantitatively, qualitatively, and relationally determined representations.

In this way, the latter headings presuppose the application (or at least applicability) of the former headings.

The next diagram connects these fundamental logical resources of the understanding (in the narrow sense) as the capacity for conecpts leading to the fundamental logical resources of reason as the capacity to draw inferences. These are themselves grounded in functions of reason, which are constituted by certain exercises of the functions of relation (of the understanding) to order judgments in syllogisms. The corresponding categorical, hypothetical, and disjunctive syllogisms have as constituent parts (more specifically as their initial or "major" premises) judgments according to the categorical, hypothetical, and disjunctive logical forms, as indicated by the dotted lines.

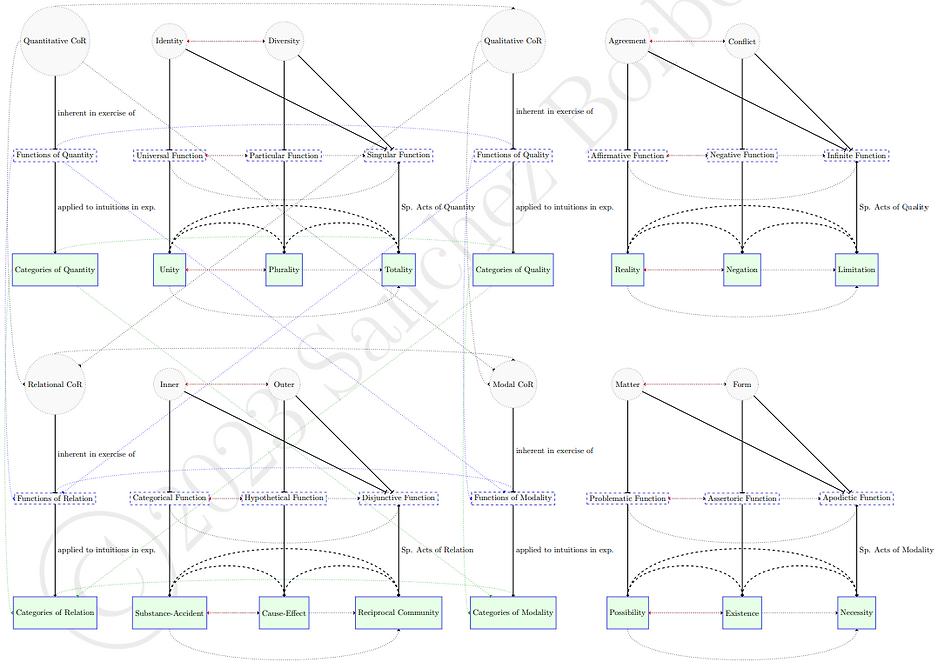
The next diagram turns from merely including logical structures to now including metaphysical structures, showing connections between individual concepts of reflection, logical functions of the understanding, and categories of nature/pure concepts of the understanding. Here again, each first and second function treats representations according to the first and second corresponding concept of reflection, while the third function treats representations according to both concepts of reflection.

Each category is basically generated by applying the corresponding function to order intuitions (though there are slight complications due to additional structure between the categories, which I explain below).

Note that the first element in each heading (be it a concept of reflection, a logical function, or category) conditions the ones that follow (as indicated by the dotted arrow). The second element opposes the first one (as indicated by the reverse red dotted arrow), and the third element (when available) combines aspects of the first and the second elements (as indicated by the two dotted arrows going to it).

There is additional structure between the categories (indicated by the upper curved dashed lines) because each second category contains the first one as a component, and each third category contains the combination of the first two categories as its components. In particular, the second category under each heading emerges from ordering the first category (and intuitions thought using it) by applying the second corresponding function. The third category under each heading, in turn, emerges from the application of the third corresponding logical function to combine the first two corresponding categories (and intuitions thought using this concept) in what Kant calls a "special act of the understanding." In my research, I argue that each category is thus generated in a special act of the understanding that applies the relevant logical function to order the relevant representations (intuitions in general and, as the case may be, previous categories in their heading).

The below diagram adds (as above) the connections constituting a progression between the general headings in the form of thin dotted reverse arrows, indicating how, e.g., the exercise of functions (or categories) of Modality presupposes the application/applicability of functions (or categories) of Quantity, Quality, and Relation, while the applicability/application of functions (or categories) of Quantity is presupposed by the exercise of functions under the subsequent headings.

The next diagram adds the transcendental schemata of the power of judgment to the previous diagram corresponding to each heading. These unique representations are, as Kant calls them, "transcendental time determinations." As transcendental or pure, these schemata are homogeneous with the purely intellectual categories. As time determinations, they are homogeneous with sensible intuitions. Thus, they play an indispensable mediating role between the content of sensibility and that of understanding, allowing intuitions sensed through forms of sensibility to be subsumed under pure concepts of the understanding. Their being temporal determinations (and thus essentially involving time) is indicated by their relation in dark pink lines to time. Although Kant does not himself represent these in the table, I have gathered them into an annotated one.

The below diagram adds (as above) the connections constituting a progression between the general headings in the form of thin dotted reverse arrows, indicating how, e.g., the schema of Modality presupposes the application of the schemata of Quantity, Quality, and Relation, while the application of the schema of Quantity is presupposed by the application of all other schemata.

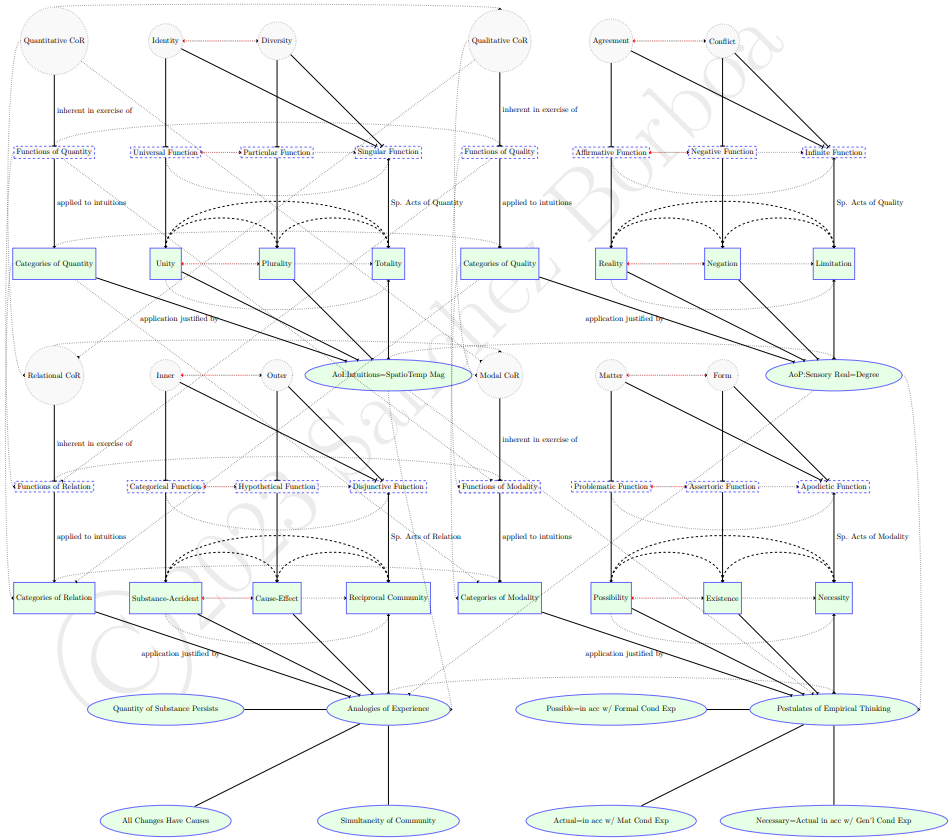
The next diagram omits the transcendental schemata and instead adds the principles of pure understanding corresponding to each heading: the axioms of intuition (for quantity), anticipations of perception (for quality), analogies of experience (for relation), and postulates of empirical thinking (for modality). These principles essentially give the conditions under which the categories can be applied to sensible objects (of which we have intuitions). The principles under each heading concern the applicability of the relevant categories. These principles thereby justify the applicability of each of the categories to what we sense in intuition, as indicated by solid reverse arrows, so as to make experience possible. Collectively then, these principles determine the formal conditions of the possibility of objective experience, where (objective) experience for Kant is "empirical cognition" i.e., the successful cognitive grasp of empirical objects by jointly sensing them (through intuitions) and thinking of them (through concepts). These formal conditions concern, roughly, the form that our activities as subjects that are things in themselves must take to make experience possible. There are additionally, material conditions of the possibility of experience that concern, roughly, the contribution that mind-independent reality must make in order to make experience possible. On a conditional constitutive interpretive approach to Kant's critical philosophy, Kant does not offer any arguments concerning the material conditions of the possibility of experience, as they lie beyond the philosophical reach of human reason.

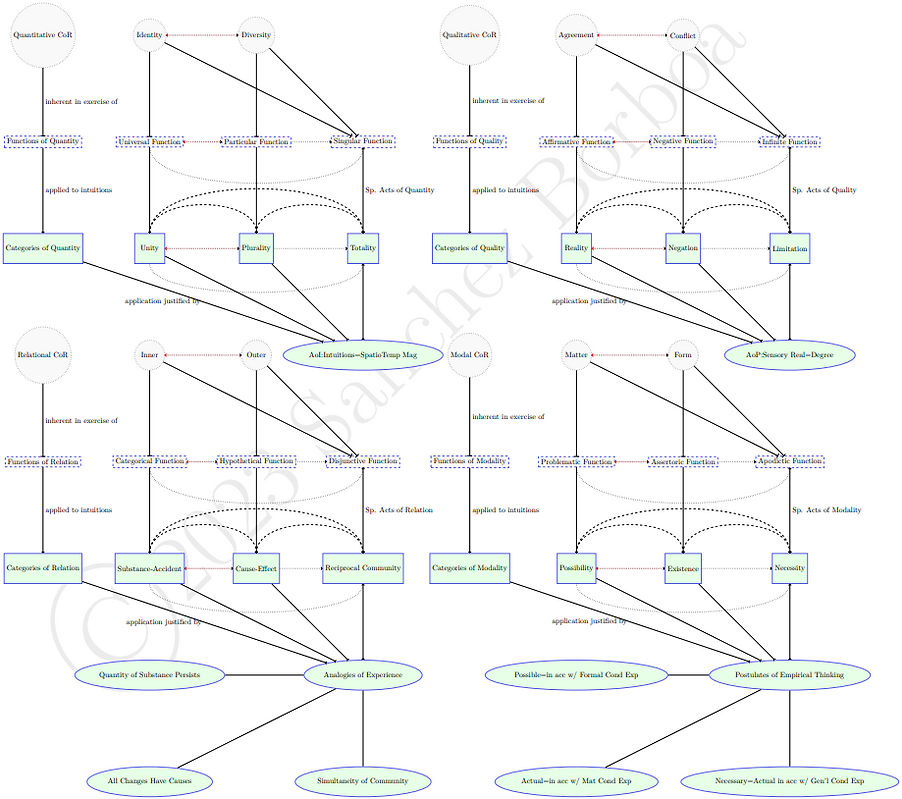
Note: This table is 'physiological' in being related to the investigation of nature (physis, the Greek for nature).

The diagram below once again adds the connections constituting progression between the general headings in the form of thin reverse dotted arrows. This indicates that e.g., the analogies of experience (and the arguments Kant gives for them) presuppose the anticipations of perceptions and the axioms of intuition.

The next diagram combines the connections between categories, transcendental schemata, and principles of pure understanding, as well as their relation to the forms of sensibility (space and time) (which ground the possibility of sensing objects by means of spatiotemporal perceptual representations).

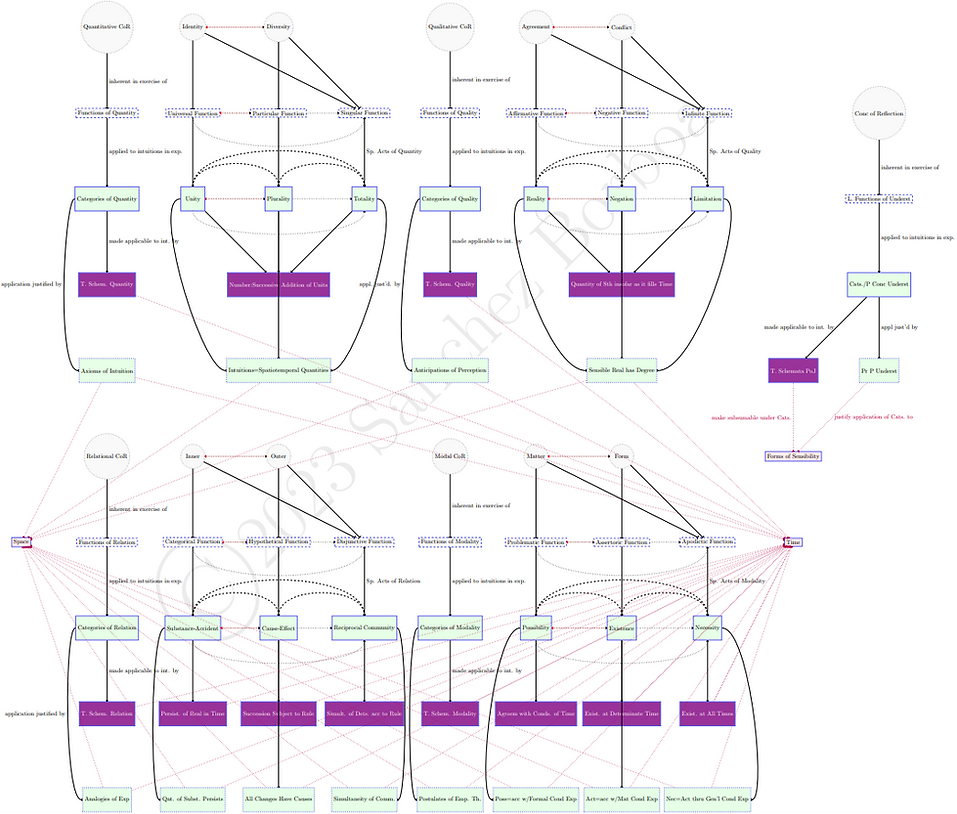
The next diagram adds the usual connections constituting a progression between headings.

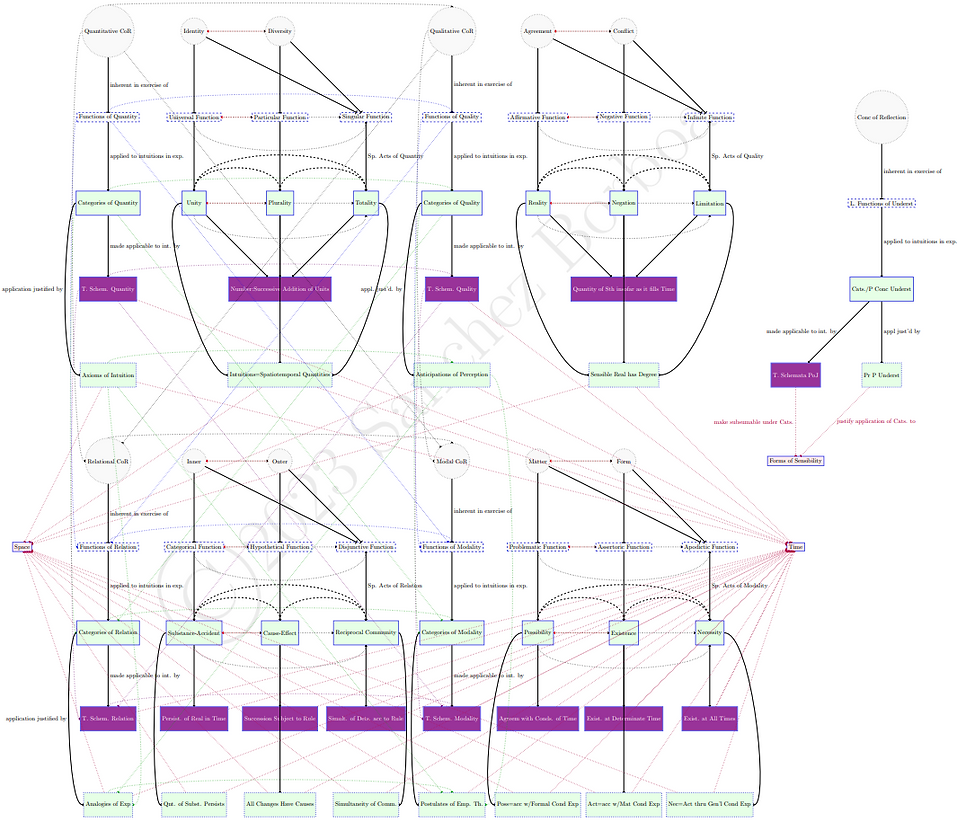
The next set of diagram omits the connections between the categories and the architectonic elements treated in the Transcendental Analytic of Principles (the transcendental schemata and principles of pure understanding) and instead connects the basic architectonic elements of the Transcendental Analytic of Concepts to the basic architectonic elements treated in the Transcendental Dialectic. The first diagram adds the functions and syllogisms/inferences of reason, also explicitly representing how it is reason's fundamental principle of seeking the unconditioned (roughly seeking ultimate, unifying explanations) that leads it to order judgments (that themselves order concepts) in syllogisms.

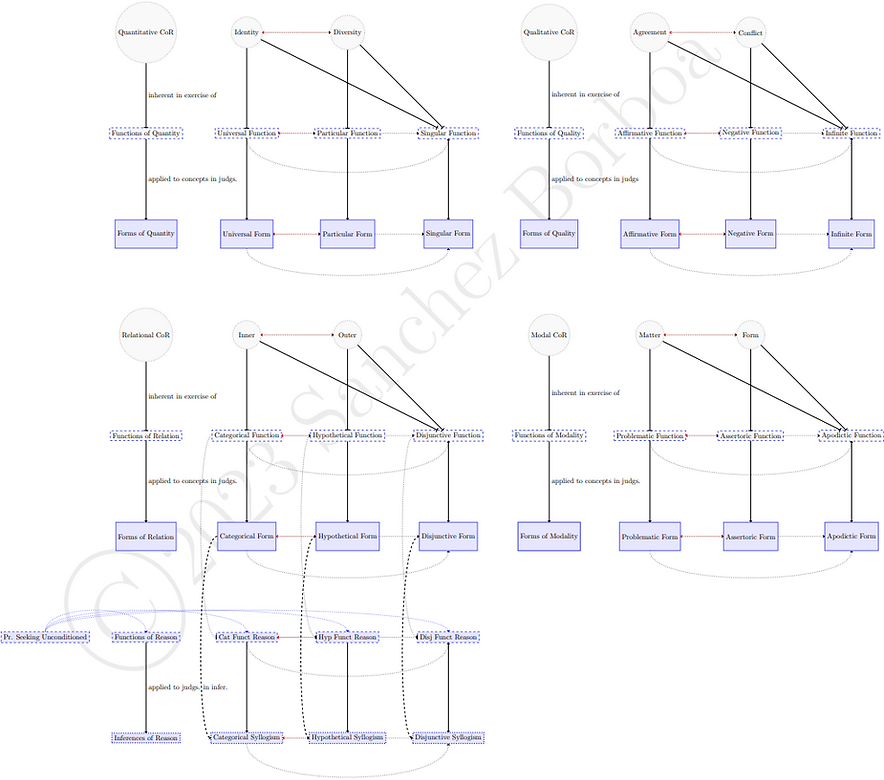
The next diagram adds the usual connections constituting a progression between the headings of the tables of the Analytic of Concepts in dotted lines and a supplementary explanatory view detailing the general pattern that plays out across headings.

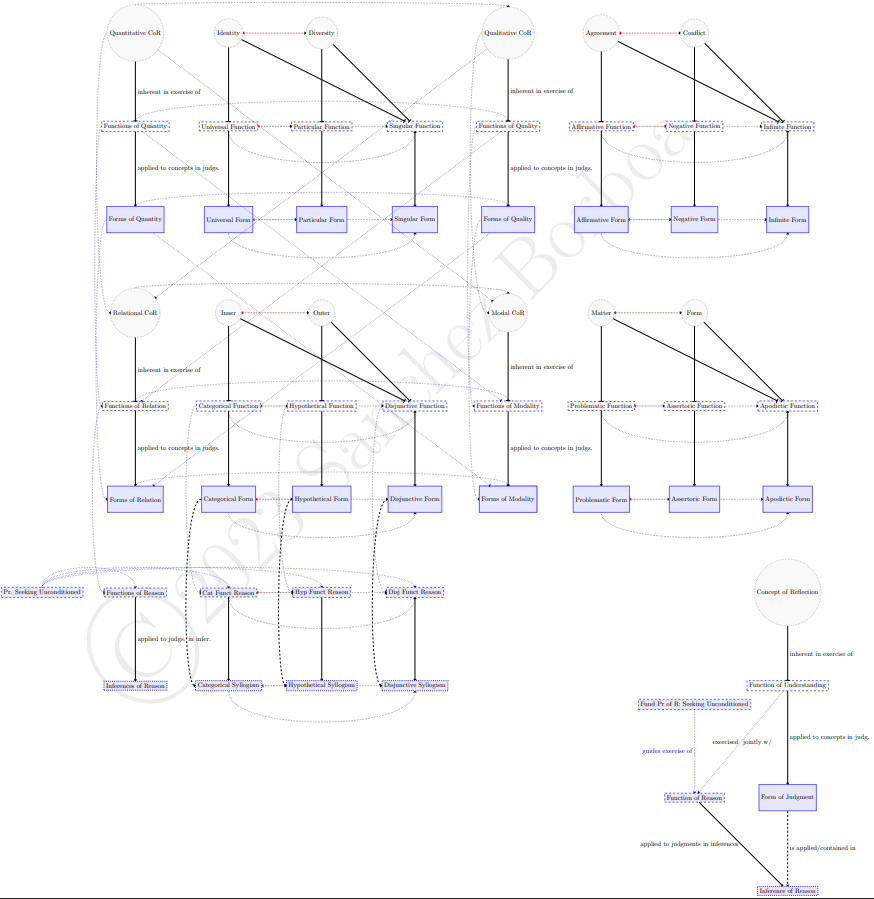
The next diagram omits the logical inferences of reason and instead connects the transcendental ideas of reason with the fundamental resources of the understanding leading to the categories (treated in the Transcendental Analytic of Concepts). When the functions of reason are exercised to seek the unconditioned in order to systematically unify experience, they generate the ideas of reason as applications of the categories beyond sensory experience. The dashed arrows indicate that the ideas of reason contain certain categories as components.

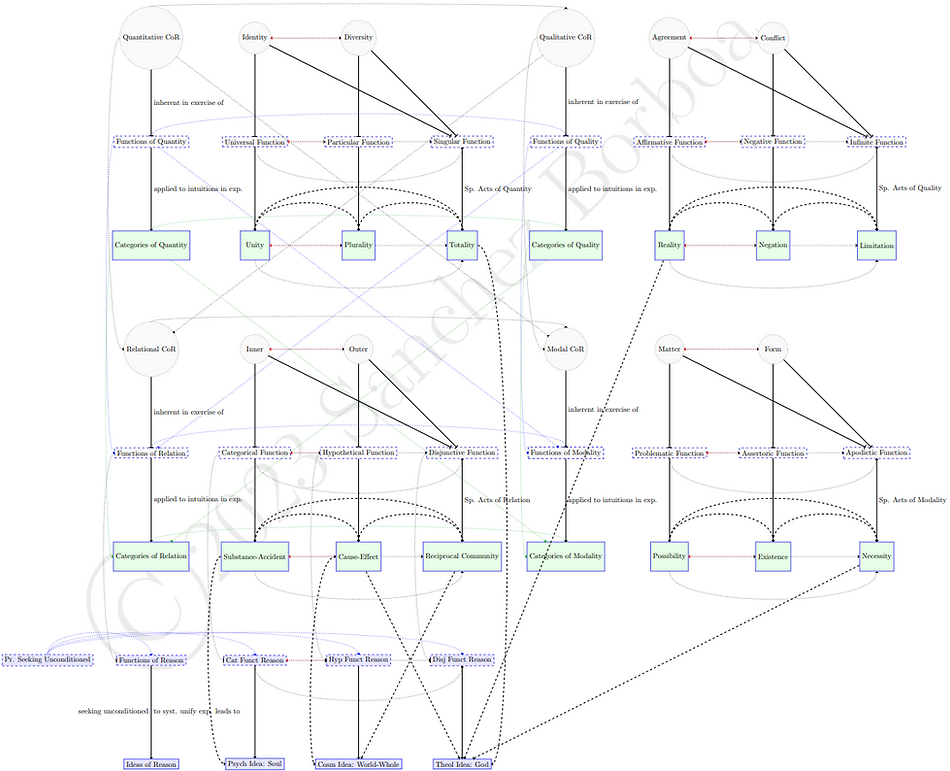
The next diagram omits all headings of the tables of functions/categories except relation and adds connections to the fallacious dialectical inferences that reason is naturally and essentially misled into when trying to use the psychological, cosmological, and theological ideas that stem from its nature. The paralogisms of the soul and proofs of the existence of God, and the "mathematical" antinomies (of quantity and quality) are all fallacious according to Kant (as indicated by dotted yellow outlines). However, the dynamical antinomies (of relation and modality) each have a thesis that correctly applies to things in themselves (indicated by a black outline) and antithesis that correctly applies to things as appearances (indicated by a green outline).

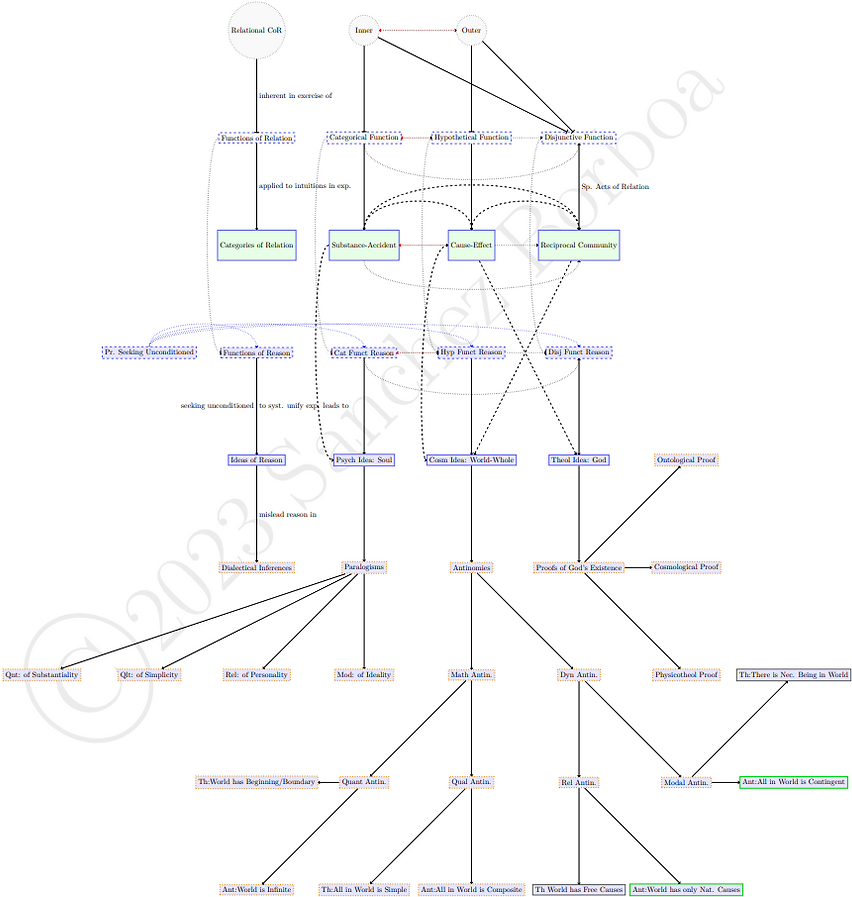
The next diagram adds all the rest of the headings for functions and categories, showing connections between them and the antinomies, as well as a supplementary explanatory view detailing the general pattern across headings/dialectical inferences.

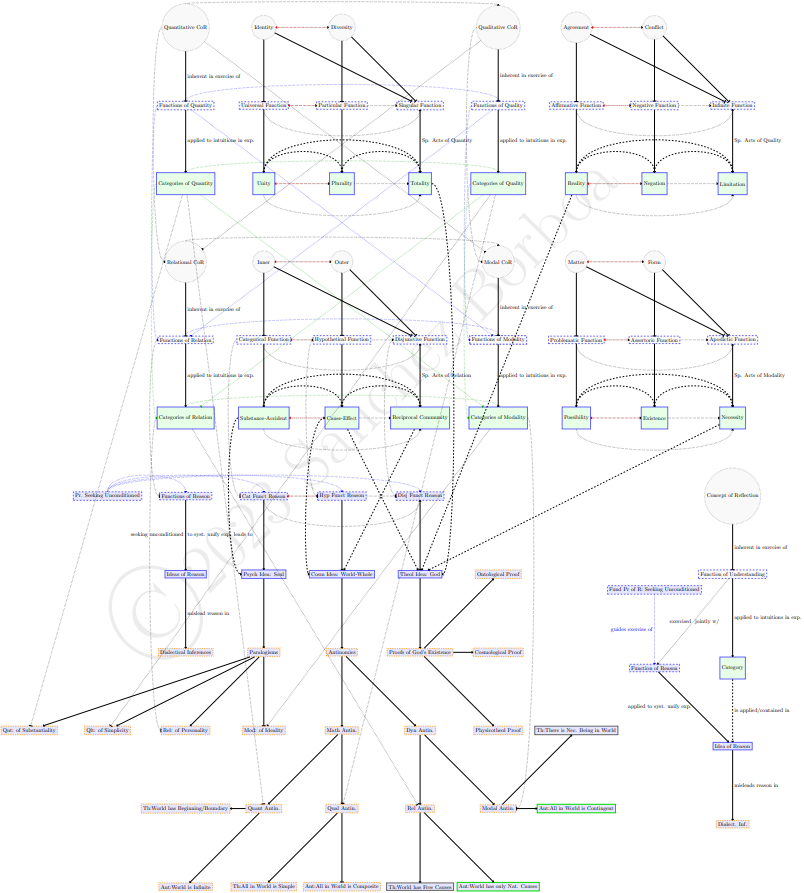
For more information of how these architectonic resources play a role in Kant's Critique of Pure Reason, you can turn here.